Der Winkel zwischen der Geraden g und der Ebene E ist der Winkel zwischen g und der Projektionsgeraden s.
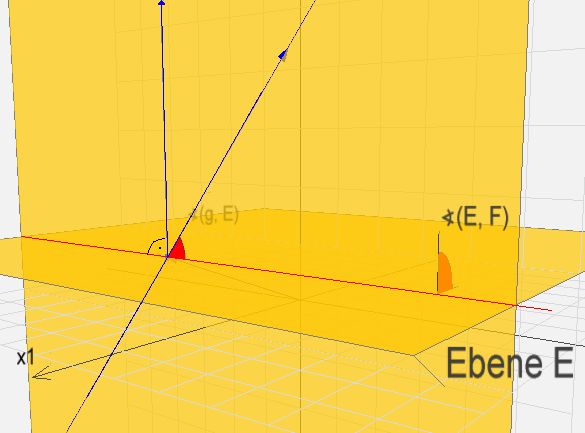
Sehen Sie sich das Bild noch einmal genau an!
Der Vektor, dessen Pfeil blau eingezeichnet ist und vom Schnittpunkt der Ebene E und der Geraden g "nach Oben" zeigt,
zeigt genau in die Projektionsrichtung, aus der die Gerade g auf die Ebene E projiziert wurde.
Er steht nach unserer Bedingung für die Projektion senkrecht zur Ebene E.
Einen solchen Vektor nennen wir Normalenvektor
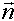 der Ebene E.
der Ebene E.Der Normalenvektor liegt auch in der Ebene F, denn diese steht ebenfalls nach unserer Forderung senkrecht auf E.
Die Projektionsgerade s, und damit ein Pfeil der ihren Richtungsvektor repräsentiert, liegt ebenfalls in der Ebene F
(und weil sie auch in E liegt muss sie senkrecht zu
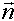 sein).
sein).Wir haben also drei Vektoren in der Ebene F:
Den Normalenvektor
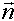 ,
,den Richtungsvektor der Geraden g
und den Richtungsvektor der Geraden s.
Wir wollen den Winkel zwischen s und g berechnen, kennen aber keine Gleichung der Geraden s.
Wir wissen aber, dass der Winkel zwischen s und
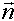 genau 90° beträgt. Sie stehen senkrecht aufeinander!
genau 90° beträgt. Sie stehen senkrecht aufeinander!Wenn wir also den Winkel zwischen g und
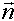 berechnen können,
berechnen können,erhalten wir aus der Differenz zu 90° den Winkel zwischen s und g, der wie wir schon wissen dem Winkel zwischen g und E entspricht.
| Definition: Der Winkel zwischen einer Ebene und einer die Ebene schneidende Geraden ist 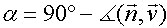 , ,wobei 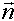 ein Normalenvektor der Ebene E und ein Normalenvektor der Ebene E und 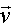 der Richtungsvektor der Geraden g ist. der Richtungsvektor der Geraden g ist. |
Wäre die Ebenengleichung bereits in Normalenform angegeben,
könnten wir den Winkel zwischen der Ebene E und der Geraden g direkt berechnen.
| Links zur besseren Navigation: | |||
| Home | Winkel oder Abstand | Skalarprodukt | Betrag |
| Normalenform | Normalenvektor | Definition Abstand | Definition Winkel |