Berechnen eines Normalenvektors einer Ebene mit dem Vektorprodukt:
Definition: Zu zwei Vektoren 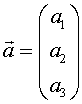 und und 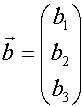 heißt das Produkt: heißt das Produkt: 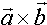 Vektorprodukt oder Kreuzprodukt von 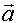 und und  . . Dabei gilt: 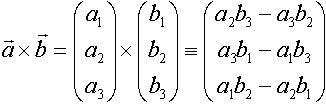 . .(Sprechweise: a kreuz b) |
Das Vektorprodukt ist ein Vektor, der senkrecht auf beide Vektoren
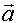 und
und 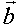 steht.
steht.Überprüfen sie das an einem Beispiel.
Beachten Sie auch das Skalarprodukt zweier aufeinander senkrecht stehender Vektoren.
| Links zur besseren Navigation: | |||
| Home | Winkel oder Abstand | Skalarprodukt | Betrag |
| Normalenform | Normalenvektor | Definition Abstand | Definition Winkel |